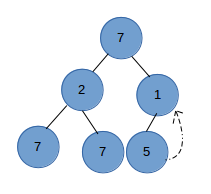
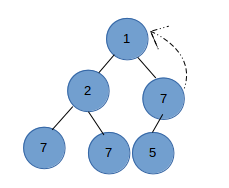
什么是Heap¹ ?

数据结构中的Heap是一种满足heap property的树:

父节点和子节点按照给定顺序，并应用在整棵树上

根据父节点和子节点不同顺序又可以分为：

min-heap(最小堆)：
1. 父节点比子节点小
2. 最小值在根节点
max-heap(最大堆)：
1. 父节点比子节点大
2. 最大值在根节点

最小堆示例

比较常用的堆是二叉堆，在结构上是一个complete binary tree。因此，对于N个节点的二叉堆，高度是 logN 。二叉堆不同于二叉查找树，即按照in-order遍历不会使数据有序，二叉堆每个节点和它的silblings并没有什么关系。

数据结构中的Heap不要和memory中的heap混淆。

更详细的信息可以参考wikipedia

为什么要用到Heap¹?

通过上面对Heap的了解，我们可以知道下面几种情况可能比较适合使用Heap:

需要sort或partially sort的应用
需要取极值的情况
需要优先级的场景

常用的priority queue其实就是用Heap来实现的。

怎么实现?

由于heap是complete binary tree, 如果使用数组来实现，那么我们知道一个node的index, 怎么知道左右child呢? 根据complete binary tree我们可以得到:

left = 2 * index ， right = 2 * index + 1

Heap上常用的操作

find-min/find-max : 取得极值

根据heap property可知, 只需要返回root节点即可

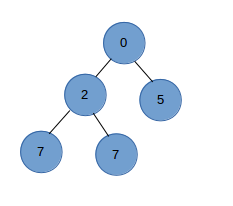
extract-min/extract-max : 删除极值

要删除root节点, 首先我们可以用最后一个节点覆盖root节点，然后比较新的root节点和左右子节点来rebalance 二叉堆

假设我们二叉堆是这样的

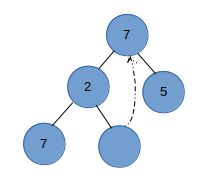
首先我们用the last node覆盖root节点

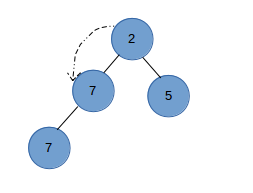
然后比较新的root节点和左右节点，交换父节点和左子节点来保持heap property

如果交换后左子树违反heap property，则重复上面步骤，只到整个二叉堆满足heap property

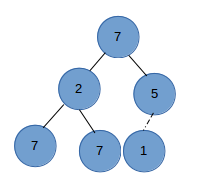
insert ：插入一个值，可能violate heap property，需要rebalance 二叉堆

要插入一个值，我们可以先作为最后一个节点，然后与父节点比较

假设我们二叉堆是这样的

首先将新值作为最后一个节点

与父节点比较发现违反heap property，则与父节点交换

重复上面步骤知道满足heap property

empty/size : 需要得到heap大小或判断是否为空
replace : 替换一个值，需要重新rebalance

代码

根据上面分析，我们可以很方便的写出二叉堆的实现，下面是我用C++的实现代码。

二叉堆的类声明如下:

template<typename T, typename comparator = std::less<T> >
class heap {
public:

    // empty arguments constructor
    heap(comparator cmp = comparator());
    // one argument constructor ( default comparator )
    heap(const std::vector<T> &nums, comparator cmp = comparator());
    // iterator constructor

    // copy constructor
    heap(const heap *other);

    // assign constructor
    const heap &operator=(const heap *other);

    // find min/max
    const T top() const;

    // extract top
    void pop();

    // insert value
    void push(T val);

    // size -- returns the number of elements
    const size_t size() const;

    // empty -- checks whether the heap is empty
    const bool empty() const;

    // destructor
    ~heap();

private:
    std::vector<T> data;
    comparator comp;
    void percolateDown(int idx);
    void percolateUp(int idx);
};

上面的二叉堆类的一个默认参数的构造函数:

// one default argument constrctor
template<typename T, typename comparator>
heap<T,comparator>::heap(comparator cmp) : comp(cmp) {
    // just initialize the data to size 1
    data.resize(1);
    //this->comp = cmp;
}

二叉堆的两个参数构造函数（第二个参数有默认值):

// two argument constructor
template<typename T, typename comparator>
heap<T, comparator>::heap(const std::vector<T> &nums, comparator cmp) {
    this->data.resize(nums.size()+1);
    this->comp = cmp;

    // copy nums to data
    copy(nums.begin(), nums.end(), data.begin()+1);
    // balance the heap
    for(int idx = this->size()/2;idx > 0;--idx)
        percolateDown(idx);
}

复制构造函数，需要deep copy数据:

// copy constructor
template<typename T, typename comparator>
heap<T,comparator>::heap(const heap *other) {
    copy(other->data.begin(), other->data.end(), this->data.begin());
    this->comp = other->comp;
}

赋值构造函数，和复制构造函数类似，需要deep copy，另外需要返回本身引用:

// assign constructor
template<typename T, typename comparator>
const heap<T,comparator>& heap<T,comparator>::operator =(const heap *other) {
    copy(other->data.begin(), other->data.end(), this->data.begin());
    this->comp = other->comp;
    return this;
}

Destructor函数:

// destructor
template<typename T, typename comparator>
heap<T,comparator>::~heap() {
}

top()函数实现，只需要在数据非空情况下返回第一个数据即可:

// find-min/max
template<typename T, typename comparator>
const T heap<T,comparator>::top() const {
    if( !empty() )
        return data[1];
}

pop()函数，由于要删掉极值，要重新rebalance二叉堆。我们用最后一个值覆盖极值，并重新build二叉堆:

// remove the top element
template<typename T, typename comparator>
void heap<T,comparator>::pop() {
    if( !empty() ) {
        data[1] = data[size()];
        data.resize(size());
        percolateDown(1);
    }
}

push()函数，我们把要插入值加入到数据后面，并根据二叉堆property来重新balance二叉堆:

// insert an element
template<typename T, typename comparator>
void heap<T,comparator>::push(T val) {
    this->data.push_back(val);
    percolateUp(size());
}

empty()函数，指示二叉堆是否为空:

// check whether the heap is empty
template<typename T, typename comparator>
const bool heap<T,comparator>::empty() const {
    return this->size() == 0;
}

size()函数，返回二叉堆的大小:

// get the size of the heap
template<typename T, typename comparator>
const size_t heap<T,comparator>::size() const {
    return this->data.size() - 1;
}

percolateDown(int idx)函数，根据二叉堆属性把数据往下移来rebalance二叉堆:

// private functions
// affter extracting root value, rebalance the heap
template<typename T, typename comparator>
void heap<T,comparator>::percolateDown(int idx) {
    if( idx > this->size()/2 )
        return;
    int midx = idx;
    if( comp(data[2*idx],data[midx])  )
        midx = 2 * idx;
    if( 2 * idx + 1 <= this->size() && comp(data[2*idx+1],data[midx]) )
        midx = 2 * idx + 1;
    if( midx != idx ) {
        std::swap(data[midx], data[idx]);
        percolateDown(midx);
    }
}

percolateUp(int idx)与上面函数相反，把数据往上移来rebalance二叉堆:

// after insert new element into heap, we need percolateup the element to
// rebalance the heap
template<typename T, typename comparator>
void heap<T,comparator>::percolateUp(int idx) {
    if( idx <= 1 )
        return;
    if( comp(data[idx] , data[idx/2]) ) {
        std::swap(data[idx], data[idx/2]);
        percolateUp(idx/2);
    }
}

以上是priority queue使用heap结构完整实现, 接下来我用实现的二叉堆做了常用的堆排序代码如下：

#include<iostream>
#include "Heap.hpp"
#include<cstddef>
#include<cstdlib>
#include<algorithm>
#include<random>

using namespace std;
void gen_array(int n, vector<int> & data, int base_start = 1, int base_end = 99) {
  srand((unsigned int)time(NULL));
  for(int i = 0; i < n; i++)
    data.push_back( rand() % (base_end - base_start) + base_start );
}

void print_array(vector<int> & data, const string s) {
  cout << s << " : ";
  for(int i = 0; i < data.size(); i++)
    cout << data[i] << " ";
  cout << endl;
}

void heapSort(vector<int> &nums) {
    heap<int> pq(nums);
    nums.resize(0);
    while(!pq.empty() ) {
        nums.push_back(pq.top());
        pq.pop();
    }
}

int main() {

      cout << "test one argument constructor and top() && pop() member function\n";
      vector<int> nums;
      srand((unsigned int)time(NULL));
      int n = rand() % 27;
      gen_array(n, nums);
      print_array(nums,"Data");
      heapSort(nums);
      print_array(nums,"Sort");

      // C++ random number generator
      // common use case: binding a RNG with a distribution
      default_random_engine e;
      uniform_int_distribution<> d(0, 10);
      function<int()> rnd = std::bind(d, e); // a copy of e is stored in rnd

      cout << "test push() member function\n";
      nums.push_back(rnd());
      heap<int> pq(nums);
      pq.push(rnd());
      nums.resize(0);
      while(!pq.empty() ) {
          nums.push_back(pq.top());
          pq.pop();
      }
      print_array(nums,"Sort");

      cout << "test max-heap\n";
      nums.push_back(rnd());
      heapSort_reverse(nums);
      print_array(nums,"Sort");

      cout << "test default no-argument constructor\n";
      heap<int> emptyPQ;
      int k = rnd();
      cout << "Data = ";
      for(int i = 0; i < k; ++i) {
          int val = rnd();
          cout << val << "\t";
          emptyPQ.push(val);
      }

      cout << endl << "Sort = ";
      while(!emptyPQ.empty() ) {
          cout << emptyPQ.top() << "\t";
          emptyPQ.pop();
      }
      cout << endl;

      return 0;
}

上面测试程序输出：

test one argument constructor and top() && pop() member function
Data : 37 60 29 43 52 81 15 35
Sort : 15 29 35 37 43 52 60 81
test push() member function
Sort : 0 1 15 29 35 37 43 52 60 81
test max-heap
Sort : 0 1 8 15 29 35 37 43 52 60 81
test default no-argument constructor
Data = 5	2	0	7	7
Sort = 0	2	5	7	7

如果没有特别说明，本文Heap都是指二叉堆 ↩ ↩²

志飞 / 2016-03-08
Published under (CC) BY-NC-SA

什么是Heap1 ?

为什么要用到Heap1?

怎么实现?

Heap上常用的操作

代码

什么是Heap¹ ?

为什么要用到Heap¹?