Red-Black Tree

什么是Red-Black Tree ?

上面说过，在最坏情况下，BST会退化成link-list，其时间复杂度是O(n)。因此为了保证O(logn)的时间复杂度，需要设计一种能够使Tree保持平衡的机制。这儿的Red-Black Tree就是一种自平衡的二叉查找树。 Red-Black Tree是符合下面定义的二叉树:

任意节点值比其左子树所有节点值大，比右子树所有节点小。(BST的定义)

任意节点要么是黑色要么是红色

根节点必须是黑色

所有的叶子节点(nil)都是黑色

如果一个节点是红色，则其左右子节点必须是黑色

从任意节点到叶子节点(nil)所有path上的黑色节点个数相同

上面说满足这些约束的就是Red-Black Tree，是能够保证O(logn)最坏时间复杂度的自平衡的二叉查找树。真的是这样吗？假设从一个节点到叶子节点的path上黑色节点个数(不算叶子节点)为B,则最长path上能够有的最多的节点个数为2*B(黑红节点交叉)，而最短的path上的节点最少也要有B个(全是黑色节点)。因此对于一个Red-Black Tree, 没有path会比其他path长两倍。这就保证了Red-Black Tree的高度大致保持平衡，而Red-Black Tree上各种操作和高度是

Red-Black Tree的实现

既然Red-Black Tree也是二叉查找树，自然能够在BST上实现的操作必然能够在Red-Black Tree上实现:

插入, 有插入数据我们才能进行其他操作
删除, 删除不需要的值
查找, 由于BST的性质，我们知道在BST上可以实现二分查找
遍历, 对于BST来讲，就是in-order-traversal了

查找和遍历由于没有写操作，和BST上相关操作一致即可。而插入和删除由于改变了树可能会违反Red-Black Tree约束，需要一些额外操作来使树重新满足约束。

代码

首先，我们声明一个RBT类, 包含上面所描述的四种操作。我们使用TreeNode作为RBT的节点,和上面的BST<T>类似。

// Binary search Tree declaration
template<typename T>
class RBT {
public:
    // default constructor
    explicit RBT();
    // copy constructor
    RBT(const RBT &other);
    // assignment constructor
    const RBT<T>& operator=(const RBT &other);
    // destructor
    ~RBT();

    enum Color { RED, BLACK };
    // TreeNode definition
    class TreeNode {
    public:
        friend class RBT;
        T val;
        TreeNode *left;
        TreeNode *right;
        TreeNode *parent;
        // indicate this node's color
        Color color;
        // constructor
        TreeNode() : left(nullptr), right(nullptr), parent(nullptr), color(BLACK){};
        TreeNode(T v) : val(v), left(nullptr), right(nullptr), parent(nullptr), color(RED){};
        TreeNode(T v, TreeNode *l, TreeNode *r, TreeNode *p = nullptr, Color c = RED) : val(v), left(l), right(r),parent(p), color(c){};
    };


    // STL-style iterator
    class iterator {
    public:
        friend class RBT;
        explicit iterator();
        const iterator& operator=(const iterator &other); // assignment constructor
        iterator& operator++(); // prefix increment
        iterator operator++(int); // postfix increment
        T& operator*() const; // derefence the pointer
        bool operator!=(const RBT<T>::iterator &other) const;
        bool operator==(const RBT<T>::iterator &other) const;
        // for iterator_traits to refer
        typedef std::output_iterator_tag iterator_category;
        typedef T value_type;
        typedef std::ptrdiff_t difference_type;
        typedef T* pointer;
        typedef T& reference;
    private:
        iterator(TreeNode* n);
        TreeNode* node;
        TreeNode* lastNode;
    };

    // iterator begin() and end()
    iterator begin() const;
    iterator end() const;

    // insert an element into RBT
    void insert(T v);

    // find an element
    iterator find(const T& v) const;
    //const_iterator find(const T& v) const;

    // remove one element
    void erase(iterator itr);

    // return the size of RBT
    const std::size_t size() const;

    // check whether the RBT is nullptr
    const bool empty() const;

private:

    int cnt;
    TreeNode *root;

    // private insert helper function
    void insert(T v, TreeNode *&r, TreeNode * const &p = nullptr);
    void insert_case1(TreeNode *r);
    void insert_case2(TreeNode *r);
    void insert_case3(TreeNode *r);
    void insert_case4(TreeNode *r);
    void insert_case5(TreeNode *r);
    TreeNode* grandParent(TreeNode * const &r) const;
    TreeNode* uncle( TreeNode * const &r) const;
    TreeNode* sibling( TreeNode * const &r) const;
    // private : replace node in parent
    void replace_node_in_parent(TreeNode *node, TreeNode *newNode = nullptr);

    // delete helper functions
    void delete_case1(TreeNode *node);
    void delete_case2(TreeNode *node);
    void delete_case3(TreeNode *node);
    void delete_case4(TreeNode *node);
    void delete_case5(TreeNode *node);
    void delete_case6(TreeNode *node);

    // rotate the node
    void rotate_right(TreeNode *r);
    void rotate_left(TreeNode *r);
    // private : find the max value node
    TreeNode *findMax(TreeNode *node);
};

RBT<T>::iterator实现, 这一部分与BST一样

// RBT<T>::iterator
// default constructor
template<typename T>
RBT<T>::iterator::iterator() {
    node = nullptr;
    lastNode = nullptr;
}

// one argument constructor
template<typename T>
RBT<T>::iterator::iterator(TreeNode* n) {
    node = n;
    lastNode = nullptr;
}

// assignment constructor
template<typename T>
const typename RBT<T>::iterator& RBT<T>::iterator::operator=(const iterator &other) {
    this->node = other.node;
    return *this;
}

template<typename T>
T& RBT<T>::iterator::operator*() const {
    return this->node->val;
}

// overload operator ==
template<typename T>
bool RBT<T>::iterator::operator==(const RBT<T>::iterator &other) const {
    return this->node == other.node;
}

// overload operator !=
template<typename T>
bool RBT<T>::iterator::operator!=(const RBT<T>::iterator &other ) const {
    return this->node != other.node;
}

// overload prefix ++
template<typename T>
typename RBT<T>::iterator& RBT<T>::iterator::operator++() {
    // if current node is root , we could get the lastNode
    if( node->parent == nullptr ) {
        lastNode = node;
        while( lastNode->right )
            lastNode = lastNode->right;
    }
    if( node->right != nullptr ) {
        node = node->right;
        while( node->left )
            node = node->left;
    } else if( node == lastNode ){
        node = nullptr;
    } else if( node == node->parent->left ) {
        node = node->parent;
    } else if( node == node->parent->right ) {
        while( node->parent->val <= node->val )
            node = node->parent;
        node = node->parent;
    }
    return *this;
}

// overload postfix ++
template<typename T>
typename RBT<T>::iterator RBT<T>::iterator::operator++(int) {
    // if current node is root , we could get the lastNode
    if( node->parent == nullptr ) {
        lastNode = node;
        while( lastNode->right )
            lastNode = lastNode->right;
    }
    TreeNode *p = this->node;
    if( node->right != nullptr ) {
        node = node->right;
        while( node->left )
            node = node->left;
    } else if( node == lastNode ){
        node = nullptr;
    } else if( node == node->parent->left ) {
        node = node->parent;
    } else if( node == node->parent->right ) {
        while( node->parent->val <= node->val )
            node = node->parent;
        node = node->parent;
    }
    return iterator(p);
}

RBT<T>无参数构造函数

// default constructor -- only initialize the private variable
template<typename T>
RBT<T>::RBT() {
    cnt = 0;
    root = nullptr;
}

RBT<T>复制构造函数，需要实现deep copy

// copy constructor -- deep copy every element of the other RBT
template<typename T>
RBT<T>::RBT(const RBT &other) {
    cnt = other.cnt;
    if( cnt == 0 )
        return;
    std::queue<std::pair<TreeNode*, TreeNode*> > q;
    q.push(std::make_pair(root(other.root->val),other.root));
    while( !q.empty() ) {
        TreeNode *node1 = q.front().first;
        TreeNode *node2 = q.front().second;
        q.pop();
        if( node2->left ) {
            node1->left = new TreeNode(node2->left->val);
            node1->left->parent = node1;
            q.push(make_pair(node1->left, node2->left));
        }
        if( node2->right ) {
            node1->right = new TreeNode(node2->right->val);
            node1->irght->parent = node1;
            q.push(make_pair(node1->right, node2->right));
        }
    }
}

RBT<T>赋值构造函数，与复制构造函数一样

// assignment constructor
template<typename T>
const RBT<T>& RBT<T>::operator=(const RBT &other) {
    cnt = other.cnt;
    if( cnt == 0 )
        return *this;
    std::queue<std::pair<TreeNode*, TreeNode*> > q;
    q.push(std::make_pair(root(other.root->val),other.root));
    while( !q.empty() ) {
        TreeNode *node1 = q.front().first;
        TreeNode *node2 = q.front().second;
        q.pop();
        if( node2->left ) {
            node1->left = new TreeNode(node2->left->val);
            node1->left->parent = node1;
            q.push(make_pair(node1->left, node2->left));
        }
        if( node2->right ) {
            node1->right = new TreeNode(node2->right->val);
            node1->right->parent = node1;
            q.push(make_pair(node1->right, node2->right));
        }
    }
    return *this;
}

RBT<T> destructor函数，当对象不需要时释放内存

// destructor
template<typename T>
RBT<T>::~RBT() {
    if( cnt == 0 )
        return ;
    cnt = 0;
    std::queue<TreeNode*> q;
    q.push(root);
    while( !q.empty() ) {
        root = q.front();
        q.pop();
        if( root->left ) {
            q.push(root->left);
        }
        if( root->right ) {
            q.push(root->right);
        }
        delete root;
    }
}

RBT<T>的size()和empty()函数

size()函数返回当前BST<T>中的元素个数

// return the size of RBT
template<typename T>
const std::size_t RBT<T>::size() const {
    return cnt;
}

empty()函数，当BST<T>没有数据时返回true

// check whether the RBT is nullptr
template<typename T>
const bool RBT<T>::empty() const {
    return cnt == 0;
}

RBT<T>的begi()和end()函数，分别返回对应的iterator

begin()函数需要首先找到BST<T>类的最左节点，然后返回其iterator实例

// iterator begin() and end()
template<typename T>
typename RBT<T>::iterator RBT<T>::begin() const {
    TreeNode* node = root;
    while( node && node->left )
        node = node->left;
    return iterator(node);
}

end()直接返回null iterator即可

template<typename T>
typename RBT<T>::iterator RBT<T>::end() const {
    return iterator();
}

实现insert(T v)来插入一个新的数据

对于insert(T v)来说，我们可以和BST<T>一样，使用二分法将数据作为leaf node插入RBT<T>。和BST<T>不同的是，插入元素默认是RED node之后还要满足RBT的规则要求

// insert an element into RBT
template<typename T>
void RBT<T>::insert(T v) {
    insert(v,root);
    // increase cnt
    ++cnt;
}

// private : insert an element into RBT
template<typename T>
void RBT<T>::insert(T v, TreeNode *&r, TreeNode * const &p) {
    if( r == nullptr ) {
        r = new TreeNode(v, nullptr, nullptr, p);
        // here we need to remove the violation of RBT if exists
        insert_case1(r);
    } else if( v < r->val )
        insert(v, r->left, r);
    else
        insert(v, r->right,r);
}

当插入的元素作为root节点，我们只需要将节点改成BLACK

// this function handle case that the current node is the root
template<typename T>
void RBT<T>::insert_case1(TreeNode *r) {
    // in this case we just paint the node to black
    if( r->parent == nullptr )
        r->color = BLACK;
    else
        insert_case2(r);
}

当插入节点的父节点是BLACK node,新插入节点没有违反RBT规则，不需要操作

// this handles when the node's parent is black
template<typename T>
void RBT<T>::insert_case2(TreeNode *r) {
    // in this case we just return
    if( r->parent->color == BLACK )
        return;
    else
        insert_case3(r);
}

如下图所示，当插入节点parent node和uncle node都是RED时，我们可以将parent node和uncle node改成BLACK,grandparent node改成RED,这样只有grandparent node违反RBT规则。所以需要从insert_case1()开始检查grandparent node。

// this handles when both the parent and the uncle are red
template<typename T>
void RBT<T>::insert_case3(TreeNode *r) {
    // when both the parent and the uncle are red, we can paint the parent and
    // uncle to black and the grandParent to red
    // this will remain all RBT rules but the grandParent may violate rule
    TreeNode* u = uncle(r);
    if( u && u->color == RED ) {
        r->parent->color = BLACK;
        u->color = BLACK;
        u->parent->color = RED;
        insert_case1(u->parent);
    } else
        insert_case4(r);
}

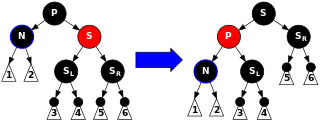
如下图所示，当插入节点parent node是RED，而uncle node都是BLACK时，如果当前节点是左子树而其父节点是右子树，我们可以在父节点上进行rotate_right()操作。如果相反，则进行rotate_left()操作。

// this handles when current node's parent is red but the uncle is black
template<typename T>
void RBT<T>::insert_case4(TreeNode *r) {
    TreeNode *g = grandParent(r);
    // when current node is the right child and parent is the left child of
    // grandParent , we rotate left
    if( r == r->parent->right && r->parent == g->left ) {
        rotate_left(r->parent);
        r = r->left;
    // in this case we rotate right
    } else if( r == r->parent->left && r->parent == g->right ) {
        rotate_right(r->parent);
        r = r->right;
    }
    insert_case5(r);
}

rotate_left(TreeNode *r)操作，就是将当前节点的右子树作为父节点而当前节点作为其左子树。

// this rotate the current node to the left
template<typename T>
void RBT<T>::rotate_left(TreeNode *r) {
    TreeNode *saved_right_left = r->right->left, *child = r->right;
    if( r->parent ) {
        if( r == r->parent->left )
            r->parent->left = child;
        else
            r->parent->right = child;
    // if current node is the root we need update the root node also
    } else {
        root = child;
    }
    child->left = r;
    child->parent = r->parent;
    r->parent = child;
    r->right = saved_right_left;
    if( saved_right_left )
        saved_right_left->parent = r;
}

rotate_right(TreeNode *r)操作，就是将当前节点的左子树作为父节点而当前节点作为其右子树。

// thi rotate the current node to the right
template<typename T>
void RBT<T>::rotate_right(TreeNode *r) {
    TreeNode *saved_left_right = r->left->right, *child = r->left;
    if( r->parent ) {
        if( r == r->parent->left )
            r->parent->left = child;
        else
            r->parent->right = child;
    // if current node is the root we need update the root node also
    } else {
        root = child;
    }
    child->right = r;
    child->parent = r->parent;
    r->parent = child;
    r->left = saved_left_right;
    if( saved_left_right )
        saved_left_right->parent = r;
}

如下图所示，当插入节点parent node是RED，而uncle node都是BLACK时，我们可以将grandparent node变成RED,而父节点变成BLACK。如果当前节点和父节点都是左子树，对grandparent node进行rotate_right()操作，这样整个RBT<T>就满足所有平衡规则了。如果当前节点和父节点都是右子树则相反。

// this handles that the parent is red but uncle is black
template<typename T>
void RBT<T>::insert_case5(TreeNode *r) {
    TreeNode *g = grandParent(r);
    // in this case we just paint the parent to BLACK and grandParent to RED
    // then rotate left or right
    g->color = RED;
    r->parent->color = BLACK;
    if( r == r->parent->left )
        rotate_right(g);
    else
        rotate_left(g);
}

grandParent(TreeNode * const &r)函数得到当前节点的grandparent node

// get current node's grandparent
template<typename T>
typename RBT<T>::TreeNode* RBT<T>::grandParent(TreeNode * const &r) const {
    if( r && r->parent )
        return r->parent->parent;
    else
        return nullptr;
}

uncle(TreeNode * const &r)函数得到父节点的兄弟节点

// get current node's uncle
template<typename T>
typename RBT<T>::TreeNode* RBT<T>::uncle(TreeNode * const &r) const {
    TreeNode *g = grandParent(r);
    // if no grandParent then no uncle
    if( g == nullptr )
        return nullptr;
    if( r->parent == g->left )
        return g->right;
    else
        return g->left;
}

find(T v)查找数据是否存在, 与BST一致，只需要二分查找即可

// find an element
template<typename T>
typename RBT<T>::iterator RBT<T>::find(const T& v) const {
    TreeNode *p = root;
    while( p ) {
        if( p->val == v )
            return iterator(p);
        if( p->val < v )
            p = p->right;
        else
            p = p->left;
    }
    return end();
}

erase(iterator itr)删除数据

对于删除元素，和insert(T v)类似，可以先按照BST<T>的方法来处理，不过类似的，除此之外，当删除节点是BLACK时候还需要额外操作来保证满足RBT<T>的规则。当要删除的节点存在RED节点时我们只需要将其改成BLACK即可。

// remove one element
template<typename T>
void RBT<T>::erase(iterator itr) {
    --cnt;
    if( cnt == 0 ) {
        delete root;
        root = nullptr;
        return;
    }
    // if left & right child both exist
    if( (itr.node)->left && (itr.node)->right ) {
        TreeNode *predecessor = findMax((itr.node)->left);
        (itr.node)->val = predecessor->val;
        erase(iterator(predecessor));
    } else {
        TreeNode *child = (itr.node)->left ? (itr.node)->left : (itr.node)->right;
        // here difference with bst, we need rebalance rbt to satisfy rbt rules
        if( (itr.node)->color == BLACK ) {
            // when current node is black and its child is RED, we can
            // simply repaint child to black
            if( child && child->color == RED )
                child->color = BLACK;
            // or the deleted node is the leaf cell, we should rebalance it
            else
                delete_case1(itr.node);
        }
        replace_node_in_parent(itr.node, child);
        delete itr.node;
    }
}

当要删除节点是root node时不需要任何操作

template<typename T>
void RBT<T>::delete_case1(TreeNode *node) {
    // when current node is the new root , it's okay
    if( node->parent != nullptr )
        delete_case2(node);
}

如下图所示，当当前节点的兄弟节点是RED时可以交换父节点与其兄弟节点的颜色。如果当前节点是左子树则对其父节点进行rotate_left()操作。反之则相反。

template<typename T>
void RBT<T>::delete_case2(TreeNode *node) {
    // in this case when current node's sibling is RED, we should replace its
    // parent's color with its sibling, and rotate the parent
    TreeNode *s = sibling(node);
    if( s->color == RED ) {
        node->parent->color = RED;
        s->color = BLACK;
        if( node == node->parent->left )
            rotate_left(node->parent);
        else
            rotate_right(node->parent);
    }
    delete_case3(node);
}

对于下图所示RBT<T>，如果当前节点兄弟节点，父节点以及兄弟节点的左右子节点都是BLACK，我们可以将其兄弟节点改成RED。

template<typename T>
void RBT<T>::delete_case3(TreeNode *node) {
    // in this case current node and its parent, its sibling and its sibling's
    // two children are both black. we just repaint its sibling to red and
    // rebalance the tree for its parent
    TreeNode *s = sibling(node);
    if( node->parent->color == BLACK && s->color == BLACK &&
        (s->left == nullptr || s->left->color == BLACK) && (s->right == nullptr || s->right->color == BLACK) ) {
        s->color = RED;
        delete_case1(node->parent);
    } else {
        delete_case4(node);
    }
}

下图所示是父节点是RED而兄弟节点及其左右子节点都是BLACK，这种情况下我们只需要交换父节点和兄弟节点颜色即可。

template<typename T>
void RBT<T>::delete_case4(TreeNode *node) {
    // in this case current node and its sibling and its sibling's two children
    // are all black but the parent is red, we can just exchange the parent and
    // its sibling's color

    TreeNode *s = sibling(node);
    if( node->parent->color == RED && s->color == BLACK &&
        (s->left == nullptr || s->left->color == BLACK) && (s->right == nullptr || s->right->color == BLACK) ) {
        s->color = RED;
        node->parent->color = BLACK;
    } else {
        delete_case5(node);
    }
}

对于下图所示情况，即当前节点兄弟节点是BLACK,如果有一个RED左子节点和BLACK右子节点可以交换兄弟节点及其左子节点的颜色，并对兄弟节点进行rotate_right()。反之则相反。

template<typename T>
void RBT<T>::delete_case5(TreeNode *node) {
    // in this case current node's sibling has a left red child and right black
    // child, we can perform a right rotation on the sibling and exchange the
    // color with its red child
    TreeNode *s = sibling(node);
    if( s->color == BLACK ) {
        if( node == node->parent->left && (s->left && s->left->color == RED) &&
            (s->right == nullptr || s->right->color == BLACK) ) {
            s->color = RED;
            s->left->color = BLACK;
            rotate_right(s);
        } else if( node == node->parent->right && (s->right && s->right->color == RED) &&
                    (s->left == nullptr || s->left->color == BLACK) ) {
            s->color = RED;
            s->right->color = BLACK;
            rotate_left(s);
        }
    }
    delete_case6(node);
}

对于下图所示情况，我们交换兄弟节点与父节点颜色，如果当前节点是左子节点，将兄弟节点右子节点改成BLACK，然后对父节点rotate_left()

template<typename T>
void RBT<T>::delete_case6(TreeNode *node) {
    // in this case current node's sibling has a right red child
    // we can perform rotate on current node's parent and exchange the color
    // with sibling, and repaint the sibling's right red child to black
    TreeNode *s = sibling(node);
    s->color = node->parent->color;
    node->parent->color = BLACK;
    if( node == node->parent->left ) {
        s->right->color = BLACK;
        rotate_left(node->parent);
    } else {
        s->left->color = BLACK;
        rotate_right(node->parent);
    }
}

与BST<T>一样，用子节点替换父节点

template<typename T>
void RBT<T>::replace_node_in_parent(TreeNode *node, TreeNode *newNode) {
    if( node->parent ) {
        if( node->parent->left == node )
            node->parent->left = newNode;
        else
            node->parent->right = newNode;
    } else {
        root = newNode;
    }
    if( newNode )
        newNode->parent = node->parent;
}

findMax(TreeNode *node)返回当前节点开始最大值

template<typename T>
typename RBT<T>::TreeNode *RBT<T>::findMax(TreeNode *node) {
    while( node && node->right )
        node = node->right;
    return node;
}

sibling(TreeNode * const &r)函数得到当前节点的兄弟节点

// get current node's silbing
template<typename T>
typename RBT<T>::TreeNode* RBT<T>::sibling(TreeNode * const &r) const {
    if( r == nullptr || r->parent == nullptr )
        return nullptr;
    if( r->parent->left == r )
        return r->parent->right;
    else
        return r->parent->left;
}

测试程序

template<typename T>
void testTree() {
    cout << endl;
    int n = rand()%5;
    int i = 0;
    while( i++ < n ) {
        T bst;
        cout << "###########" << endl;
        cout << "Test step : " << i << endl;
        int m = rand()%10;
        cout << "insert : ";
        int v;
        while( m-- ) {
            v = rand()%100;
            cout << v << "\t";
            bst.insert(v);
        }
        cout << endl << "bst = ";
        typename T::iterator itr = bst.begin();
        while( itr != bst.end() ) {
            cout << *itr << "\t";
            itr++;
        }
        itr = bst.begin();
        if( itr != bst.end() ) {
            cout << endl << "after erase " << *itr << endl << "bst =";
            bst.erase(itr);
        }
        itr = bst.begin();
        while( itr != bst.end() ) {
            cout << *itr << "\t";
            itr++;
        }
        int x = v;
        itr = bst.find(x);
        if( itr != bst.end() ) {
            cout << "\nFound " << x << ", now delete it" << endl;
            bst.erase(itr);
        } else {
            cout << "\nCouldn't find " << x << endl;
        }
        cout << "bst = ";
        itr = bst.begin();
        while( itr != bst.end() ) {
            cout << *itr << "\t";
            itr++;
        }
        cout << "\nbst.size() = " << bst.size();
        cout << endl << "###########" << endl;
        cout << endl;
    }
}

int main() {
    srand((unsigned int)time(NULL));
    cout << "Test BST<int>\n";
    testTree<BST<int> >();
    cout << "Test RBT<int>\n";
    testTree<RBT<int> >();
    return 0;
}

测试程序输出:

Test BST<int>

###########
Test step : 1
insert : 78	17
bst = 17	78
after erase 17
bst =78
Couldn't find 17
bst = 78
bst.size() = 1
###########

###########
Test step : 2
insert :
bst =
Couldn't find 17
bst =
bst.size() = 0
###########

Test RBT<int>

###########
Test step : 1
insert : 13	40	78	34	14	96	32	24	82
bst = 13	14	24	32	34	40	78	82	96
after erase 13
bst =14	24	32	34	40	78	82	96
Found 82, now delete it
bst = 14	24	32	34	40	78	96
bst.size() = 7
###########

###########
Test step : 2
insert : 4	82	42	87	81	28	74	54	95
bst = 4	28	42	54	74	81	82	87	95
after erase 4
bst =28	42	54	74	81	82	87	95
Found 95, now delete it
bst = 28	42	54	74	81	82	87
bst.size() = 7
###########

###########
Test step : 3
insert : 60	14	69
bst = 14	60	69
after erase 14
bst =60	69
Found 69, now delete it
bst = 60
bst.size() = 1
###########

###########
Test step : 4
insert : 62	23	15	31	34	31	22
bst = 15	22	23	31	31	34	62
after erase 15
bst =22	23	31	31	34	62
Found 22, now delete it
bst = 23	31	31	34	62
bst.size() = 5
###########

参考

1.wikipedia - binary search tree
2.wikipedia - red black tree

志飞 / 2016-03-24
Published under (CC) BY-NC-SA